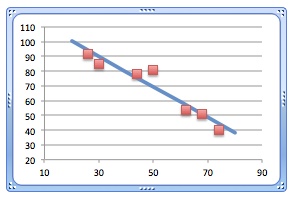
1 - Regressionsgerade und Korrelationskoeffizient
Löschen Sie die Statistikregister mit CLEAR. Geben Sie folgende Wertepaare ein (jeweils y ENTER x, gefolgt von Σ+):

Drücken Sie L.R. und rollen Sie den Stack, um alle Resultate zu sehen.

Die Regressionsgerade ist definiert durch y = -1.035x + 121.038

Der Korrelationskoeffizient ist -0.957 (starke negative Korrelation), die Kovarianz hat den Wert -354.143.

Welchen y-Wert erreicht die blaue Gerade bei x = 10?   10  x^,y^,r  = 110.691 (in Y)

Welchen x-Wert erreicht die blaue Gerade bei y = 20?   20  x^,y^,r  = 97.655 (in X)

2 - Stichproben- und wahre Standardabweichung
Die x-Werte im obigen Beispiel haben den Mittelwert 50.571 und die Standardabweichung 18.501. Die Standardabweichung ist korrekt für den Fall, dass es sich bei den sieben x-Werten um Stichproben aus einer grösseren Menge handelt. Stellen die sieben Werte aber die gesamte Menge von Daten dar, erhält man die wahre Standardabweichung, indem man den berechneten Mittelwert als weiteren Datenwert miteinbezieht:

Drücken Sie nach der Berechnung des Mittelwerts nochmals die Taste Σ+ und berechnen Sie dann den Mittelwert.

Der Mittelwert bleibt unverändert, aber die Standardabweichung wird kleiner: 17.129

3 - Lotto
Wie erzeuge ich Zahlen für das deutsche Zahlenlotto?

Sie benötigen 6 aus 49 Zahlen:

1  ENTER  49  ENTER

Wiederholtes Drücken von RAN# liefert die gewünschten Zufallszahlen (Duplikate sind möglich).

Und wieviele verschiedene Tipps sind so möglich?

4 - Ungerade Wurzel aus einer negativen Ganzzahl
Was ist die siebte Wurzel aus -2187 ?

Eingabe: 2187  CHS  ENTER  7  1/x  y^x ergibt das Resultat -3

Die meisten Taschenrechner quittieren diese Rechnung mit einer Fehlermeldung oder einem komplexen Resultat.
(Die komplexe Lösung erhält man in der Betriebsart CMPLX).

5 - Kubische Gleichung
Gesucht sind die Lösungen der Gleichung x³ - 4x² + 8x - 8 = 0

Eingabe: 1  ENTER  4  CHS  ENTER  8  ENTER  CHS  Cube

ergibt die reelle Lösung x₁ = 2.000.
Die komplexen Lösungen erhält man durch Rollen des Stacks: x_2,3 = 1.000 ± 1.732i

Überprüfen von x₂ (mit Realteil 1.000 in X und Imaginärteil 1.732i in Y):

CMPLX  ENTER  ENTER
x²  x  LastX  4  x  –
x↔y  8  x  +  8  –

6 - Lineare Gleichung mit 2 Unbekannten
Ein Vater und ein Sohn sind zusammen 62 Jahre alt. Vor sechs Jahren war der Vater viermal so alt wie damals der Sohn. Wie alt ist jeder?

Mit x = Alter des Vaters, y = Alter des Sohns:

x + y = 62
x - 6 = 4 * (y-6)

Unbekannte auf die linke Seite bringen:

1*x + 1*y  = 62
1*x - 4*y = -18

Die Koeffizienten werden wie folgt auf die Register abgebildet:

		=
1	1		62
		=
1	-4		-18

Abspeichern der Koeffizienten und Berechnung ausführen:

1  STO 4     1  STO 5     62  STO 6
1  STO 1    -4  STO 2    -18  STO 3
LinEq

Man erhält für x = 46 (Vater) und y = 16 (Sohn).

7 - Eulersche Identität
Stellen Sie die Betriebsart CMPLX ein und verifizieren Sie dann die berühmte Eulersche Identität e^iπ + 1 = 0 auf dem RPN-45:
Eingabe: π  Re↔Im  e^x  1  +  ergibt das Resultat 0.00 + 0.00i

Hier ist eine andere Form der selben Formel: π = -i ln(-1)
1  CHS  ENTER  ln  x↔y  Re↔Im  x  = 3.142 + 0.000i  = π

8 - Kubikwurzel aus einer komplexen Zahl
Was ist die dritte Wurzel aus 5 + 3i ?

Eingabe:  CMPLX  5  ENTER  3  I  3  1/x  y^x  ergibt das Resultat 1.771 + 0.322i

Für natürliche Zahlen n hat die n-te Wurzel aus einer komplexen Zahl n Lösungen. Die obige Methode zeigt nur die erste.

9 - Komplexe Zahlen in Polarform
Wie berechnet man 2(cos 65° + i sin 65°) + 3(cos 40° + i sin 40°) [Polarkoordinaten] bzw. 2∠65° + 3∠40° [Phasennotation]?
RPN-45 erwartet, dass komplexe Zahlen in kartesischen Koordinaten ausgedrückt sind. Mit →R und →∠ können die erforderlichen Umwandlungen vorgenommen werden.

Eingabe: CMPLX  DEG  2  ENTER  65  I  →R  3  ENTER  40  I  →R  +  →∠  ergibt das Resultat 4.8863(cos 49.9612° + i sin 49.9612°) bzw. 4.8863∠49.9612°

10 - Auswertung eines Ausdrucks mit komplexen Zahlen
Eine Schritt-für-Schritt-Darstellung, wie man mit RPN-45 einen Ausdruck berechnet. Der Ablauf ist praktisch der gleiche wie mit reellen Zahlen.
RPN-45 ist bereits im komplexen Modus, das Winkelmass ist Altgrad (DEG). Es sind 4 Kommastellen sichtbar (FIX 4).

Man berechne

11 - Die Funktion "DATE"
DATE berechnet den Wochentag eines Datums sowie Datum und Wochentag eines Datums für eine bestimmte Anzahl von Tagen in der Vergangenheit oder Zukunft ab einem bestimmten Datum.
ΔDYS bestimmt die Anzahl Tage vom Datum in Y bis zum Datum in X.
Der zulässige Datumsbereich ist 1.1.0001 bis 31.12.9999.

12 - Kalenderreform
Der Gregorianische Kalender wurde nur in wenigen Ländern sofort eingeführt (1582). Im Heiligen Römischen Reich war das Stichdatum beispielsweise der Tag nach dem Sonntag, 28. Februar 1700 (julianisch). Welches Datum hatte der darauf folgende gregorianische Tag?

Eingabe: -28.021700  DATE  1  DATE  ergibt das Resultat 1. März 1700 (Montag)

Die Oktoberrevolution war eigentlich eine Novemberrevolution:
Eingabe: -25.101917  DATE  0  DATE  = 7. November 1917 (Mittwoch)

13 - Die erweiterten Σ+ Funktionen
Die Taste Σ+ kann auch zusammen mit STO und RCL verwendet werden. STO  Σ+ speichert x in R7, y in R8, RCL  Σ+ holt die Werte nach x und y zurück.
Mit STO/RCL  [op]  Σ+ steht auch Registerarithmetik zur Verfügung. [op] bezeichnet dabei eine der vier Grundrechenarten (Addition, Subtraktion, Multiplikation, Division).
Auf diese Weise können 2-dimensionale Werte, z.B. Vektoren, leicht verrechnet werden.
Alle Operationen sind auch mit komplexen Zahlen durchführbar.

Beispiel: Gesucht sei die Hälfte der Summe der beiden Vektoren (6,7) und (8,11).
Eingabe: 7  ENTER  6  STO  Σ+  11  ENTER  8  STO  +  Σ+  0.5  ENTER  RCL  x  Σ+  ergibt das Resultat (7,9)

14 - Gewogener Mittelwert
Bei 30 Tankfüllungen zahlen Sie folgende Preise:

Wie gross ist der mittlere Benzinpreis?

Löschen Sie die Statistikregister mit CLEAR. Geben Sie die obigen Wertepaare ein (jeweils y ENTER x, gefolgt von Σ+).

Berechnung: x_w,s = 1.625 (mit einer Standardabweichung von y = 0.006)

15 - Bemerkenswerte Formeln
Die folgenden ungewöhnlichen Formeln können mit RPN-45 leicht verifiziert werden: